Описание случая, НЕ редкого в математическом кружке.

Детям предлагаются задачи (со спичками, со счетными палочками): выложить из определенного количества палочек фигуры; переложить указанное количество палочек и получить указанную фигуру.

Задания сложные, взятые из олимпиадных задач и у великих популяризаторов математики: Я.И.Перельмана, М.Гарднера и др.

Время от времени кого-нибудь из детей "осеняет", и фигура сложена. Остальные дети мрачнеют и повторяют построение.

Методически правильно строить занятие от простого к сложному. Сначала то, что очевидно, потом - то, над чем необходимо думать.

Например, все, без исключения, дети легко выполняют следующее задание: 

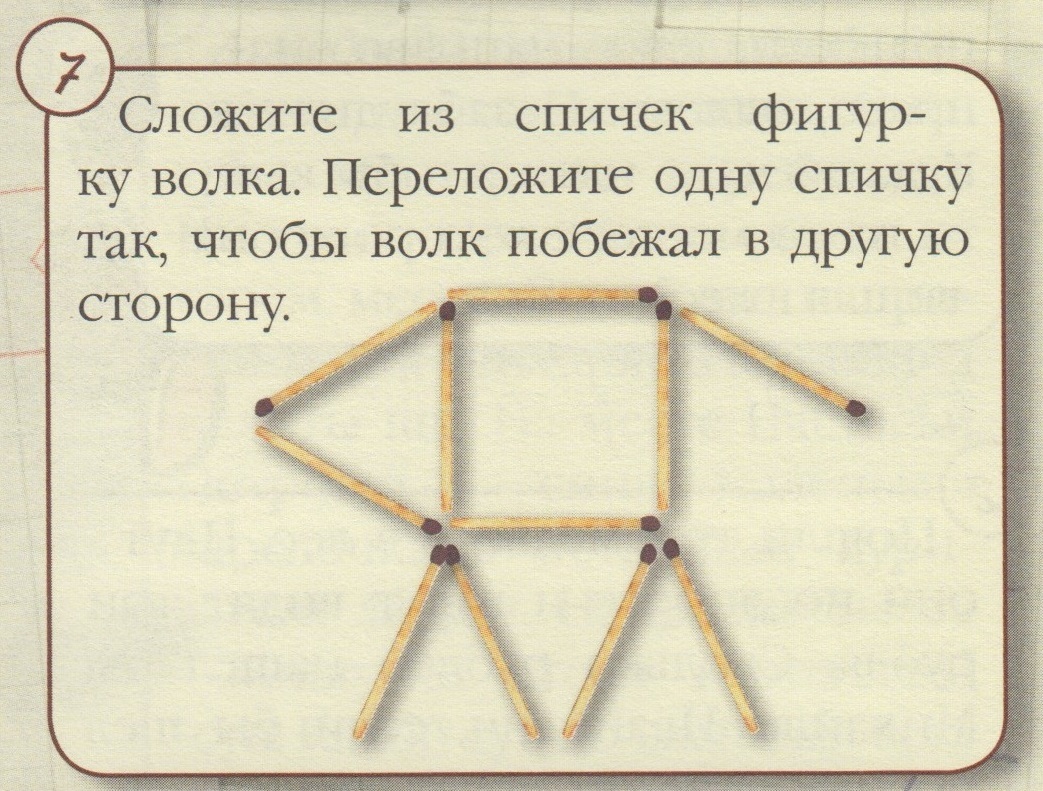
Скан из книги: Математические олимпиады в стране сказок. - М.: Белый город, 2012г. - с.9

Тогда мы добавляем фигурке рога, чтобы получилась корова:

Скан из книги: Математические олимпиады в стране сказок. - М.: Белый город, 2012г. - с.35  

Разница в 26 страниц намекает на возросшую сложность задачи.

Две (вроде бы) похожие задачи, но между ними - пропасть инерции мышления.

С первого раза преодолеть эту пропасть не удаётся, что бы мы ни делали. А делаем мы вот что: 

1) Ходим как волки туда-сюда (наблюдаем за положением тела, головы);

2) Смотрим в разные стороны как коровы (не ходим, а поворачиваем голову).

Как мы ни стараемся, не развитое у дошкольников абстрактное мышление тормозит возможность замечать отличие одной задачи от другой. Дети делают неправильные решения: то перекладывают больше палочек, то - не понимают, что делать с рогами. 

Тогда мы:

3) Находим те спички, которые составляют голову коровы (и находим среди них шею).

4) Повторяем 2)

Может быть, теперь дети смогут повернуть корове голову, не поворачивая рога? Увы, часто - нет.

На одном из занятий я показала решение: корова поворачивает голову, а рога остаются на месте. Решение готово, выложено на столе - осталось только повторить на своей корове.

С мест послышалась череда печальных вздохов и один радостный: "Я повернул голову! Я сделал это первый! Смотрите! Я первый повернул голову корове!"

Дети проигнорировали выкрики, упиваясь сожалением, а один из мальчиков мрачно ответил: "Ну и что, что первый. Не ты же решение придумал...."

ВЫВОДЫ:

1. Существуют дети, которым важно быть в движении, и делать всё быстро. В идеале - быть первым по быстроте.

2. Существуют дети, которым важно делать самим, даже если медленнее и после всех. В идеале - решить задачу.

3. Существуют дети возраста 5-ти лет, которые знают разницу между своим собственным решением и готовым.