Набор детей 5 и 6 лет в новые группы
Начало занятий: октябрь 2026
Математика для детей 5+ , г. Санкт-Петербург
Руководитель: Надежда Владимировна Братчикова
Тел. +7 (812) 954-55-44
Адрес: СПб, ул. Дыбенко д.5 к.1, центр «Искусство Мыслить Активно». Невский район, (ст.м. Дыбенко, ст.м. Проспект Большевиков)
Запись в VK-группе математического клуба ЛИСА
Родители будут включены в групповое обсуждение VK (с преподавателем) и смогут задавать вопросы.
Продолжительность занятия: 50 минут
Состав группы: 4-6 детей
Очевидные плюсы: ребёнок опередит школьную программу
Очевидные минусы: ребёнок опередит школьную программу
Цели занятий математикой:
1. Обучающая цель: новый для детей материал (количественное сравнение (развитие "чувства числа") через измерение, шкалирование; построенине элементарных геометрических понятий (точка, линия и т.п.)). Новые понятия вводятся сначала на интуитивно-наглядном уровне.
2. Развивающая цель: навыки и умения (решать задачи, уважительно общаться с коллективом детей, спокойно выигрывтаь и проигрывать в коллективных играх и пр.).
3. Воспитательная цель: развитие понимания того, что сложные проблемы, учитывая имеющиеся правила, можно разложить на ряд простых; формирование привычки делать домашнее задание и предъявлять результаты работы (проверочные, контрольные).
Воспитание - это организация жизни ребёнка. Необходимо "создать такую цепь упражнений, цепь трудностей, которые надо преодолевать и благодаря которым выходит хороший человек" (Макаренко А.С. Собрание сочинений в 8тт. – М.: 1983 – 1986. Т.7. - С.39)
На уроках математики дети развивают:
- внимание;
- терпение;
- коммуникативные способности (слушать, понимать, помогать, содействовать, возражать, спорить);
- умение логически рассуждать;
- умение алгоритмизировать задачи для последующего решения;
- умение моделировать ситуации;
- индуктивное мышление;
- дедуктивное мышление;
- критичность мышления.
На уроках математики необходимо развивать жизненно необходимые навыки:
- "Перспективного устремления" по А.С.Макаренко (постановку ближних, средних, дальних целей и "смыслов на каждой "линии" жизненных перспектив", это основа для последующей возможности ставить множество независимых и глобальныз целей).
- Вхождения в разные роли (и деятельности) и выхода из них по И. Л. Викентьеву.
- Наблюдения (в первую очередь за собой).
- Заботы о других людях и о мире (не для себя, а для более важного).
- Внимания и сосредоточения.
- Эмоциональной сферы ребёнка (научить ребёнка видеть, слышать, адекватно понимать другого человека).
- Самоконтроля и волевой сферы ребёнка.
Методические принципы преподавания математики детям:
- Изложение материала: движение от простого, частного, к общему, более сложному, повторение пройденных тем.
- Новая информация должна быть разбита на минимально возможные порции информации, каждая порция должна быть проработана.
- Стратегически важный материал и необходимые для обучения навыки должны отрабатываться до 100% усвоения.
- Усвоение полученного материала должно непрерывно контролироваться (обратная связь от родителей, проверочные и пр.).
Причины неуспеваемости детей по математике:
1. Пропуск (незнание) даже одной темы достаточен для потери смысла.
Поэтому родители участников математического клуба ЛИСА включены в чат, в котором публикуются фрагменты занятия, реакции детей, исправляются ошибки, есть возможность задавать вопросы. Даже если ребенок болеет - он не выпадает из группы.
2. Способности к освоению математики перекрывает навешание ярлыков ("двоечник").
Смысл развития не в получении оценки, а в нахождении и обязательном исправлении ошибок.
3. Уменьшение количества часов занятия математикой.
Поэтому необходимо делать домашние задания.
Родители имеют возможность наблюдать за занятием из коридора - дверь в помещение, где занимаются дети, всегда открыта, в коридоре можно поставить табуреточку.
Если вы решили остаться на занятии и понаблюдать (не вмешиваясь и не поправляя своего ребенка - удержаться подсказывать своему ребенку очень сложно), то рекомендую оценить занятия по следующим критериям:
- Уровень владения преподавателя предметом в целом.
- Общая эрудиция преподавателя и эрудиция по предмету (наличие исторических справок).
- Язык преподавателя.
- Свобода владения терминологией а) преподавателем; б) детьми.
- Научность изложения материала преподавателем.
- Наличие обратной связи от преподавателя.
- Темп занятия.
- Загрузка детей на занятии.
- Вовлечённость детей в работу на занятии.
- Элементы индивидуального подхода на занятии.
- Нормы домашнего задания.
ОТВЕТЫ на вопросы родителей

Заметка "О важном шаге родителей пятилетних детей": (читать на сайте издательства LIVREZON) https://livrezon.com/publication/nadejda-bratchikova-dnevnik-pedagoga-zapis-25-o-vajnom-shage-roditelei-pyatiletnih-detei
1. Что заставляет родителей искать математический кружок?
2. Какие приёмы заложены в методике преподавания математики для пятилетних детей?
3. В чем состоит математическое творчество?
1. "Есть ли у моего ребёнка математические способности?"
Что мы понимаем под "математическими способностями"? Какова динамика становления математических способностях и контрольные точки (возраст ребёнка), в которых математические способности проявляются?
Математические способности по академику А.Н. Колмогорову:
"1) способность умелого преобразования сложных буквенных выражений, нахождения удачных путей для решения уравнений, не подходящих под стандартные правила, или, как это принято называть у математиков, вычислительные или "алгоритмические" способности;
2) геометрическое воображение или "геометрическую интуицию";
3) искусство последовательного, правильного расчлененного логического рассуждения; в частности, хорошим критерием логической зрелости, совершенно необходимой математику, является понимание и умение правильно применять принцип математической индукции."
Крутецкий В.А. Психология математических способностей школьников / Под редакцией Н.И. Чуприковой. - М.: Издательство "Институт практической психологии"; Воронеж: Издательство НПО "МОДЭК", 1998. - с.72
2. "Зачем нужны домашние задания?"
Домашние задания для развития математических способностей необходимы, потому что развитие способностей связано с образованием множества привычек. Одна из привычек состоит в регулярности получения промежуточных результатов (выполнение домашнего задания) и их предъявление (проверочные).
3. "Как заставить ребёнка делать домашнее задание?"
Идея домашних заданий сложна для детей. Родители помогают детям делать домашние задания, выделяя время на помощь детям - присутствуя при выполнении домашнего задания. К сожалению, детям нельзя сказать "делай", и они будут делать. Взрослым придется детям помогать.
4. "Не рано заниматься математикой с детьми 5-6 лет? Почему бы не подождать до школы?"
1. Чтобы не терять времени. У вас ВСЕГО 4 ГОДА (5-9 лет)
После пяти с половиной лет начинается интенсивное формирование способности действовать в уме. Эта способность лежит в основе отличия успевающих в школе детей от неуспевающих. Чем раньше (с 5-ти лет) ребенок начинает решать задачи для развития способности действовать в уме, тем легче ему учиться, тем интенсивнее будет развиваться абстрактное мышление.
В эсперименте 1961 г. участвовали 800 школьников начальных классов и были сделаны выводы [подробнее в книге: Пономарев Я.А. Знания, мышление и умственное развитие. М.: Просвещение, 1967]:
а) К 4-му классу только половина учащихся достигает высших уровней развития способности действовать в уме.
б) Начиная с третьего класса (9 лет), к четвертому классу развитие способности действовать в уме существенно замедляется. Перестав тренировать способность действовать в уме, часть детей в 3-м и 4-х классах или совсем прекращает развитие, или чрезмерно замедляет его. Развитие некоторых детей в школе протекало успешно, а потом оно неожиданно либо вообще прерывалось (дети при этом во всех других отношениях оставались совершенно нормальными, физически здоровыми), либо деградировало.
У ребёнка всего 4 года для того, чтобы развить способность действовать "в уме". Тогда в 12 лет он сможет
✔овладевать знаниями значительной степени сложности;
✔ адекватно оперировать усвоенными знаниями.
2. 5-6 лет - это самый благоприятный, по Жану Пиаже, возраст для обучения ребенка: развивается интуитивное мышление, опирающееся на восприятие. В возрасте 5 - 6 лет ребенок активно формирует мнение о мире, т.е. строит картину мира (представление о реальности, отражающее познавательную деятельность ребенка, которое наиболее соответствует поступающей информации, поступающей в мозг через органы чувств).
5. "Зачем математика моему ребёнку?"
1. Спокойно относиться к неудачам: сомневаться, ошибаться, осознавать свои ошибки и исправлять их.
2. Давать определения: относить предмет к множеству и выделять признаки.
3. Задавать уточняющие вопросы, проясняющие непонимание, неизбежно возникающее из-за асимметричного дуализма языкового знака. Математическая польза состоит в развитии способности формулировать правильные вопросы.
4. Искать контрпримеры и опровергать теории. Подтверждающие примеры доказывают лишь справедливость частного случая. Достаточно одного контрпримера, чтобы опровергнуть всю теорию.
5. Определять границы области достоверного и невозможного, оценивать следствия.
6. Группировать и находить целое, классифицировать и определять структуру, отбрасывать несущественные данные и обнаруживать взаимосвязи между оставшимися параметрами.
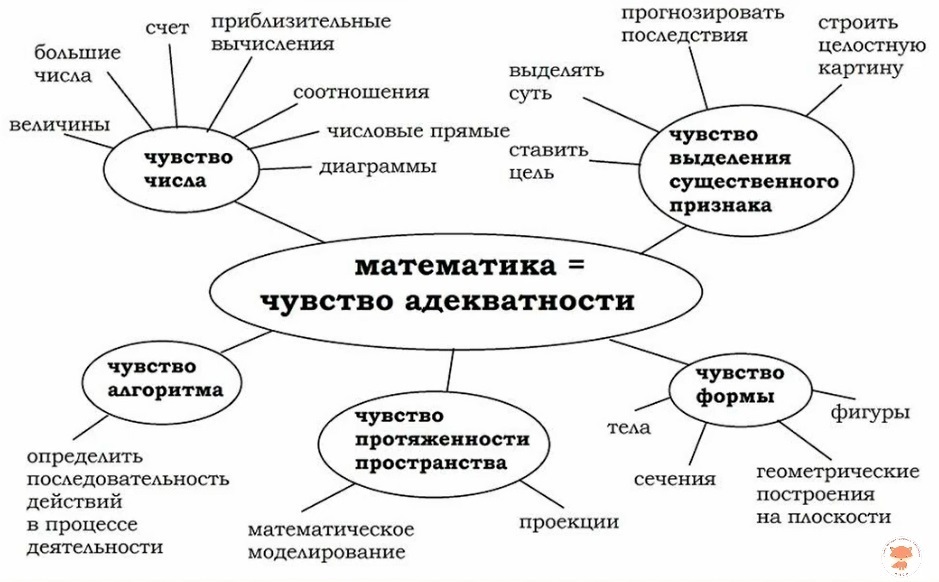
6. "Почему "ЧУВСТВО ЧИСЛА"? Мы сразу хотим конфликтологию!"
Чувство числа - это основа. Сначала чувство числа, потом переход к счету, к арифметическим операциям (до 10-ти, до 20-ти, переход через десяток), создание мысленной модели числовой прямой. Нет основы - не на чем возводить фундамент геометрии и теории вероятностей.
7. "Зачем ходить на занятия? Можно ли заниматься самим дома?"
Конечно, можно. Найдите достойную методику, приготовьте стимульные материалы и учебные пособия, подготовьте занятие и занимайтесь дома самостоятельно.
8. "Ребёнок всё делает очень медленно (очень активный). Он сможет заниматься?"
Ребёнок может быть активным по следующим причинам:
1) Биологическая причина - районы коры, ответственные за внимание и саморегулирование, менее активны, чем другие. Т.е. ребёнок не может сосредоточиться (трудно удерживать внимание) => много и беспорядочно двигается. Вероятно, наши занятия ребенку с диагнозом СДВГ не подойдут.
2) Социальная причина - ребёнок делается неусидчивым исключительно на к-л занятиях (если, например, не понимает задания). Заниматься у нас сможет.
Кроме того, у разных детей - разные темпоритмы. Одни дети быстро "загораются" и быстро теряют интерес, другие - долго "раскачиваются", а потом долго работают. На занятиях мы делаем упражнения на переключение темпоритмов, чтобы каждый из детей в течение занятия получил возможность реагировать как быстро, так и медленно.
9. "Дети будут всё занятие сидеть за партами и решать примеры?"
Конечно, нет. Однако, когда дети пишут - мы обязательно сидим за столом. Деятельность, через которую дети обучаются – моделирующая (создание наглядных моделей, установление отношений между элементами модели):
1) сюжетно-ролевые игры;
2) продуктивная деятельность (конструирование, рисование, лепка, и пр.).
10. "Мой ребёнок не любит учиться, не хочет идти в школу. Что-то можно сделать?"
Бывает так, что переутомленные бесчисленными рабочими тетрадями, без оценки собственных результатов, без сравнения своих результатов с результатами коллектива, без коллективной мотивации, к 7-ми годам дети далее "учиться" желания не имеют.
Если поместить такого ребёнка в рабочую группу детей, может "сработать" коллективная мотивация.
11. "Моему ребёнку 4 года, я хочу, чтобы он был умным. Почему кружок только для детей от 5-ти лет?"
До 5-ти лет главное, что могут сделать родители для развития интеллекта ребёнка - 1) любить, 2) организовать режим дня, 3) отдать в спортивную секцию (плавать, танцевать и т.п.). До 5-ти лет ребёнок ни физически, ни психологически не готов к ритму занятий кружка (за редким исключением).
Когда ребёнку исполняется 5 лет, его интеллект начинает активно заниматься формированием (очерчиванием границ) собственной картины мира. В картину мира им будет включено то, что описывается математическим языком. Например, если он в 5 лет не научится снижать неопределенность наблюдением, выраженном в количественных величинах (посредством измерения), с большой долей вероятности, к школе в его картине мира не будет способа справляться с тревогой неопределенности. Чем дальше по возрасту, начиная с 5-ти лет, тем у картины мира всё более и более жёсткие рамки, которые всё сложнее изменить.
Контрольный вопрос: Как Вы ведёте себя в ситуации неопределенности? Если безрассудно, значит, в возрасте 5-6 лет Вас не научили важным вещам.
12. "Мой ребёнок застенчивый. Он сможет заниматься?"
Можно сидеть с ребёнком рядом, на маленьком стульчике, столько занятий, сколько потребуется для того, чтобы ребёнок почувствовал себя безопасно в группе и мог оставаться на занятии один.
13. "Как часто нужно заниматься с ребёнком математикой?"
В группе: 50 минут, 1 раз в неделю.
Дома: Д/З - 10 минут, каждый день.
14. "Девочкам математика не нужна. Пусть ей мальчики занимаются!"
Очень может быть. Потому что даже когда ИИ (искусственный интеллект) будет работать водителем трамвая, работа мастера по маникюру (это женская профессия) точно останется человеческой профессией.
15. "У всех детей в группе будет результат?"
Результат будет у тех, кто выполняет д/з.
1) Мала вероятность, что в будущем ребёнку, вне учебы, потребуется брать определённые интегралы вручную. А дисциплина ума, умение трудолюбиво безропотно выполнять множество скучных, однообразных действий, тренировка приоритета разума над желаниями в жизни всяко пригодится.
2) Базовый навык адекватности и здравого смысла - это, во многом, результат знания математики, это "рентгеновские" очки, сквозь которые видна структура мира.
16. "У старшего ребёнка проблема с математикой в школе. Что делать?"
Начинать с начала. С чувства числа.
17. "Детям нужны курсы "подготовка к школе" в школе?"
Некоторым детям нужны. некоторым - не нужны. В среднем, обычные курсы подготовки к школе - это хорошая возможность научить ребёнка долго сидеть на стуле и привыкать к окружению средних детей.
18. "Что могут сделать родители сделать для развития ребёнка возраста 5-6 лет?"
Как минимум, научить ребёнка выделять события, которые наиболее существенно влияют на жизнь (при переходе дороги опаснее та машина, которая быстрее движется и т.д.). Как максимум, расставить семейные приоритеты: что полезнее дошкольнику: учиться красиво писать или точно оценивать ситуацию? Или и то, и другое? И пятое и десятое? От приоритетов и будет зависеть ответ на поставленный вопрос.
19. "Как научить детей принимать решения в условиях неопределенности?"
Для начала: развивать чувство числа. Чтобы ребёнок мог сравнивать.